`When I showed up at my first Twitter Math Camp in 2014 I was a ball of nerves. It was my first chance to meet, in real life, the math teachers of the #MTBoS from whom I had learned so much. I’m probably not the only person who feels nervous at their first in-real-life meeting of online friends or colleagues. What I noticed was that, while I could anticipate certain things about a person from our online interactions, having a chance to interact with them in real time and space enriched and deepened our interactions. By the end of our three days learning together, making math after hours, and chatting over a variety of meal times, I found myself with a much more nuanced understanding of my friends and colleagues.

I think it’s the same kind of situation for math learning. 

Richard Skemp defined the difference between Instrumental and Relational Understanding in math. Here’s a visual overview (via David Wees) of the difference between the two kinds of understanding:

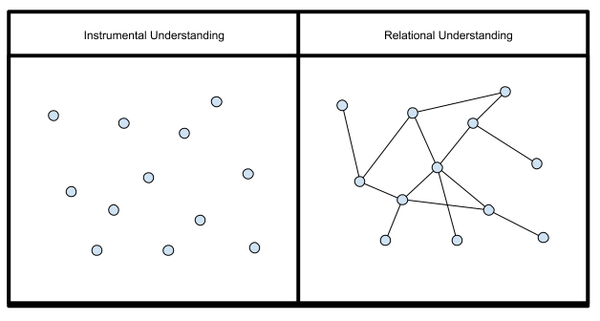
Math teacher Mark Chubb explains in his blog post Focusing on Relational Understanding:

Students who are taught instrumentally come to see mathematics as isolated pieces of knowledge. They are expected to remember procedures for each and every concept/skill.  Each new skill requires a new set of procedures.  However, those who are taught relationally make connections between and within concepts and skills.  Those with a relational understanding can learn new concepts easier, retain previous concepts, and are able to deviate from formulas/rules given different problems easier because of the connections they have made.

My perspective on relational understanding focuses getting to know a math idea in multiple contexts. Zoltan Dienes (creator of the base 10 blocks you use in your classroom) thought so too (bolding mine):

According to Dienes … mathematical abstractions occur when students recognize structural similarities shared by several related models. For example, when base-ten blocks are used to teach arithmetic regrouping operations, Dienes claimed that it is not enough for students to work with a single model; they must also investigate “mappings” to other models, such as bundling sticks or an abacus … a primary goal is to help students recognize how patterns of relationships in one model correspond to patterns of relationships in another model.

Because math is frequently presented in a static way, whether in textbooks or on worksheets, the dynamic action represented by those symbols and figures are often lost in the shuffle. The experience of math in this single mode and a series of fixed images, ideas, and answers might leave us to wonder:

How can we  learn math out of our seats? How can we learn math if its not written down? 

As part of my new First Steps series for bringing #movingmath into the classroom in a low-stress way we’re gonna’ have a TON of fun exploring math off the page in the next few months!

To kick things off let’s start by finding the math idea of scale as it exists off the page. Scale is a ratio that compares the size of one thing to another. It is what we are thinking about when we ask “how much bigger/smaller, taller/shorter, or faster/slower.” For example: In this picture of the Louisville Slugger Museum and Factory, how much bigger is the bat to the building? How much smaller is my kid compared to the giant bat?

Another example of scale off the page (which also does double duty as a great example of whole-body #movingmath) are the videos from OK GO, below.  To create the video for the song I Won’t Let You Down the music was slowed down 50% to record the complex movements at half the speed. It clocks in at about 10 minutes. The song and moving images were sped up for the final video which clocks in a little more than 5 minutes .

Overall, it’s not about whether one mode of math thinking and doing is better than another. It’s about providing opportunities for our students to really get to know a math idea in all its forms. We do this when we provide opportunities for learners to reflect on the process by which they arrived at an answer, by recognizing that watching an OK GO video during unit about scale might provide students with new insights, or by creating a lesson where students use their own bodies as measuring tools.

Whole-body math learning is one part of a whole variety of experiences that, taken together, help build a personal relationship to math so that we can recognize and rely on our new friend … on the page … and off.

Malke Rosenfeld is a dance teaching artist, author, editor, math explorer, and presenter whose interests focus on the learning that happens at the intersection of math and the moving body. She delights in creating rich environments in which children and adults can explore, make, play, and talk math based on their own questions and inclinations. Her new book Math on the Move: Engaging Students in Whole Body Learning was recently published by Heinemann (2016). Join Malke and other educators on Facebook as we build a growing community of practice around whole-body math learning.