Earlier this year I was contacted by Eric Stucky who was lecturing a course for math majors at the University of Minnesota. Although I am generally in the realm of elementary mathematics, over the years I have had the pleasure of interacting with professional mathematicians and others who think expansively about both the mathematical subject matter AND the pedagogy of their instruction.
These experiences and conversations continue to show me that whole-body math learning is for everyone. This particular story is an email conversation I had with Eric that shows just how powerful whole-body math investigations can be for fourth graders AND math majors. This is also a story about coming to understand how to negotiate a whole-body math lesson. I especially appreciate Eric’s reflections later on in this post on how his lesson went.
[ERIC]
Hello Malke,
I am a graduate student at UMN, looking for advice on an activity. I am currently a lecturer for an upper-division course for math majors; this is my first lecturing position. Class meets for two hours straight, so I’m always on the lookout for activities to break up the time.
On Wednesday, the class begins a unit on planar graphs. I had the idea to build some large physical models of graphs out of index cards [vertices] and yarn [edges], and then have them play around trying to see if they can get the edges to not cross each other.
Figuring I should know what the research is, I found your blog. Your post “A Framework for Whole-Body Math Teaching & Learning” made me consider integration of movement may not be substantial enough: they might as well lay the cards on the floor. The models should be big enough that they would have to walk/stretch to move the vertices around, but at that point, perhaps the movement becomes less of a reasoning tool and more just a nuisance? At least they would still have the experience of moving the edges physically instead of metaphorically (i.e. as they would when redrawing the graph on a worksheet), but this feels weak to me.
Unfortunately, there’s a logistical difficulty that doesn’t arise in the Rope Polygons exercise: students only have two hands, so it’s not as straightforward to make *them* the vertices of the graph because they can’t just “hold on to their edges” in a straightforward way. I really feel that if this could be done somehow, it would provide that extra something to make this activity be really special.
If you have any thoughts, or any references to point me to, I’d love to hear them. Thank you for your hard work!
-eric
[MALKE]
Hi Eric! Thanks for getting in touch. I’m excited that you are wanting to try a whole-body math activity with your students. My first thought after reading about your plans for the activity is that it’s not weak at all. Movement is important but in this case I think it’s more about the change of scale and the collaborative effort to meet a series of challenges you provide (I’m assuming you might already have a specific graph or graphs in mind?) I wonder if you could find some sturdy elastic instead of rope to make the activity more dynamic? The change of scale cannot be underestimated as a learning tool.
[ERIC]
Sorry that I left you hanging… the activity ended up getting delayed for a few weeks because of some pressing issues that we discovered from the homework, but it did end up happening! Your kind words gave me the push I needed to do it, and you were spot-on: the collaborative aspect was definitely reinforced by the change of scale [emphasis added] and I think it worked out well all around.
I ended up using the yarn thinking that I could just use multiple strands per edge, but when I was doing some test runs I realized that this was a terrible idea because it was too much work to get the strands to stay together so they ended up being single-stranded yarn strongly taped to hard-plastic plates; definitely would do that differently next time.

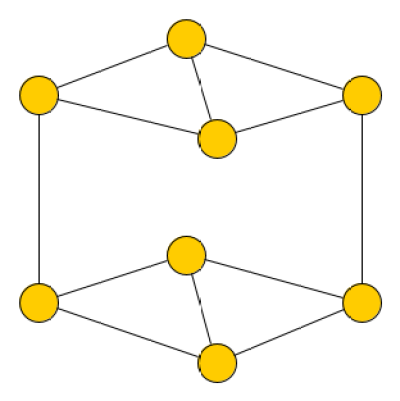
I decided to give them one non-planar graph (pictured left) to see what they would do with it. After that group worked on it for a while, and I told other people to go work on it with them, I asked the class what they thought. Half of them decided that it wasn’t possible, and half of them were not so convinced. I wonder how related those results were to how much interaction the students had with that graph. (Unfortunately, the idea was IMO undercut by the fact that one of the planar graphs I gave was a bit too complicated, and that group wasn’t able to untangle it. I didn’t tell them that it was planar— except one student who asked me about it after class. But I think everyone could see that the two groups were getting stuck in qualitatively different ways. I wonder how much the results were influenced by that graph).
The graph on the bottom right was the planar graph that the class wasn’t able to figure out.
 A further note from Eric: It was important to me that the graph to the left would be fairly hard to identify for the more advanced students. In particular, if they already knew Euler’s formula and the q≤3v-6 inequality this would be useless, because it has the same number of vertices and edges as a cube, which is planar. Moreover, although it has K_{3,3} as a minor, it does not have K_{3,3} as a subgraph, so some passing familiarity with the classic 3-utilities puzzle would not be enough to immediately detect nonplanarity. In practice, although I had a few very advanced students in my class, including one who worked on this graph from the beginning, this wasn’t an issue— or perhaps it was just a success :P)
A further note from Eric: It was important to me that the graph to the left would be fairly hard to identify for the more advanced students. In particular, if they already knew Euler’s formula and the q≤3v-6 inequality this would be useless, because it has the same number of vertices and edges as a cube, which is planar. Moreover, although it has K_{3,3} as a minor, it does not have K_{3,3} as a subgraph, so some passing familiarity with the classic 3-utilities puzzle would not be enough to immediately detect nonplanarity. In practice, although I had a few very advanced students in my class, including one who worked on this graph from the beginning, this wasn’t an issue— or perhaps it was just a success :P)
Malke Rosenfeld is a percussive dance teaching artist, Heinemann author, editor, math explorer, and presenter whose interests focus on the learning that happens at the intersection of math and the moving body. She delights in creating rich environments in which children and adults can explore, make, play, and talk math based on their own questions and inclinations.You can find out more about her work at malkerosenfeld.com, on Twitter, Instagram, or Facebook.